그래프

1. 그래프란?

• 노드(정점,vertex)랑 간선(edge)을 이용한 비선형(일렬이 아닌 것) 데이터 구조
• 데이터 관계 표현 시 사용함
• 방향성 : 간선은 방향이 있을 수도 없을 수도 있음
  • 없으면 무방향 그래프 undirected graph
  • 있으면 방향 그래프 directed graph
  • 둘다 서로 가리키는 간선도 있음
• 가중치 : 흐름의 정도
  • 가중치가 있는 그래프 : weight graph
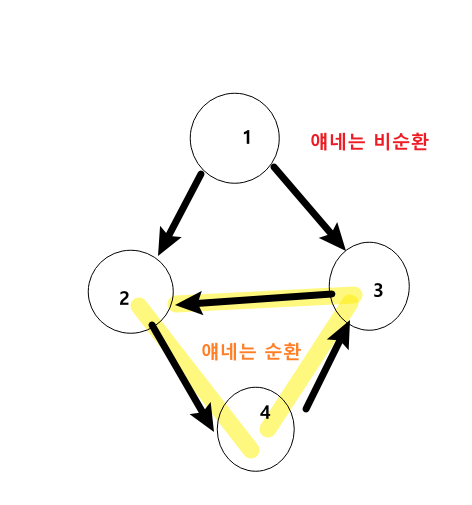
• 순환 : 다시 돌아오는 경로
  • 있으면 순환 그래프 cycle graph
  • 없으면 비순환 그래프 acyclic graph

동그라미가 노드, 화살표가 간선, 간선 위에 숫자가 가중치

 

 

2. 그래프 구현은 어떻게?

• 구현할 때 인접행렬(adjacency matrix), 인접리스트(adjacency list) 두가지 방법이 있음
• "송파역에서 석촌역으로 유동인구가 5000명 발생" 을 구현해보자
  • 데이터 담고 있는 노드 (송파, 석촌)
  • 노드 잇는 간선( 송파, 석촌 연결 유무)
  • 간선의 방향 (송파에서 석촌으로)
  • 간선의 가중치 (5000명)

정점이 2개 (송파역, 석촌역)

2.1. 인접행렬?

• 인접 행렬은 그래프를 2차원 배열(행렬)로 표현하는 방법
• 구현이 인접리스트 보다는 쉽당
• 어떻게? 정점수 * 정점수로 일단 2차원 배열 먼저 만든다
  • 예시는 2*2 임

    

• 행렬의 행과 열이 그래프의 정점(vertex) 을 나타냄
  • 이게 뭔 말이냐면..

송파에서 석촌가는 유동인구만 잇으니까 나머진 graph[0][1] = 5000, 순서는 개발자가 만드는 것, 석촌 송파 순서 바꿀 수 있음.

 

2.2. 인접리스트

• 대부분의 경우, "인접 리스트(Adjacency List)"가 더 많이 쓰임!
• 특히 정점(Vertex) 개수(N)가 많고, 간선(Edge) 개수(E)가 적을 때 훨씬 효율적
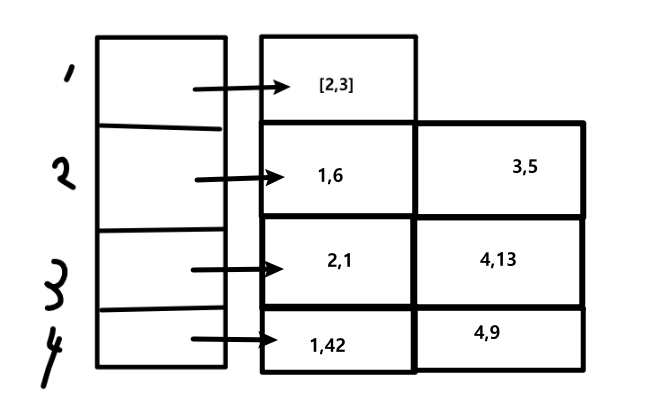
• 노드의 갯수만큼 배열 준비함 -> 그리고 리스트용 노드에는 [정점, 가중치]

노드 갯수 4개니까

배열인덱스는 시작노드, 리스트에는 [도착노드, 가중치]

마저 그려본다면..

#include <iostream>
#include <vector>
using namespace std;

struct NodeInfo {
	int NodeNum;
	int Weight;
};

vector <vector<NodeInfo>> AdjList;

//--------------------------------------
void AddEdge(int StartNode, int DestNode, int Weight)
{
	AdjList[StartNode].push_back({DestNode , Weight});
}
//--------------------------------------
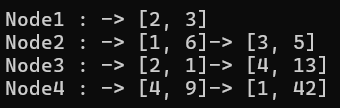
void RenderAdjList()
{
	for (int i = 1; i < AdjList.size(); i++)
	{
		cout << "Node" << i << " : ";
		for (const auto& Node : AdjList[i])
		{
			cout << "-> [" << Node.NodeNum << ", " << Node.Weight << "]";
		}
		cout << endl;
	}
}
//--------------------------------------
int main()
{
	int N = 5; //
	AdjList.resize(N);

	AddEdge(1,2,3);
	AddEdge(2,1,6);
	AddEdge(2,3,5);
	AddEdge(3,2,1);
	AddEdge(3,4,13);
	AddEdge(4,4,9);
	AddEdge(4,1,42);

	RenderAdjList();
	return 0;
}